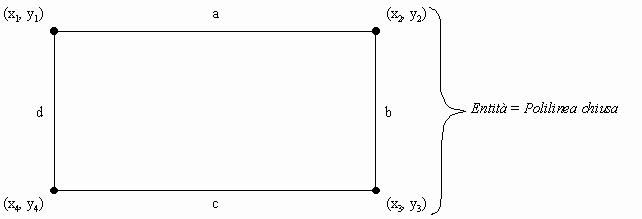Corso di Cartografia Numerica
Istituto Universitario di Architettura di Venezia
Corso di Diploma in Sistemi Informativi Territoriali (prof.ssa Alberta
Bianchin)
Lezioni ed esercitazioni a cura di Markus M.
Hedorfer
1. Che cosa sono le Strutture di Dati?
Argomento trattato durante le lezioni dell'11 e del 18 marzo 1997.
Argomenti correlati:
Sommario di questa pagina:
1. Introduzione
Joseph Berry, docente alla Colorado State University di Fort Collins
(USA), introduce in modo simpatico la questione delle strutture di dati,
illustrando quali sono le differenze nella percezione di segni grafici
tra esseri umani e calcolatori. Riporto qui di seguito un breve passaggio
di un suo articolo apparso sulla rivista specializzata GIS World.
"Per una persona, una carta è un’immagine composta da
una colorita simbologia. Quando vedi una coppia di linee rosse che si incrociano,
la tua intuizione grafica dice: "un’intersezione stradale". Quando
due linee blu si congiungono in una sola, pensi: "confluenza di un
fiume". Mentre i tuoi occhi scorrono attraverso una carta dei suoli,
facilmente capisci quali unità pedologiche sono tra loro adiacenti.
Tali verità sono lampanti. Ma questo non è il caso di una
carta computerizzata. Per il computer una carta è semplicemente
un insieme organizzato di numeri. Tutte le relazioni tra gli oggetti di
una carta devono essere archiviate all’interno dell’insieme di numeri o,
altrimenti, il computer non potrà ‘vedere’ la carta. Il termine
topologia spaziale descrive il concetto di questo collegamento e
può essere concepito come informazione aggiunta alla pila di coordinate
cartografiche."
(Joseph K. Berry, What Does Your Computer Really Think
of Your Map?, in: GIS World n.11/1994)
Del termine "topologia" si parlerà più avanti.
Intanto è utile affermare che una struttura di dati o, più
in generale, una carta numerica, può essere definita come modo
di archiviare numericamente dei dati geografici. Sebbene sia facile
incontrare, a seconda di chi scrive, delle definizioni leggermente diverse,
nella sostanza comunque non cambia molto. L’importante è capire
che il concetto di "carta", così come lo si intende tradizionalmente,
è qui poco adatto. Ma poiché i termini consolidati nel tempo
sono duri a morire, molti (me compreso) continuano ad usare questa parola
aggiungendovi semplicemente l’aggettivo "numerica".
2. Come Vengono Archiviati
gli Oggetti Grafici in un Calcolatore?
Considerando un oggetto grafico molto semplice, come un rettangolo,
si possono fare le seguenti osservazioni per quanto riguarda la percezione
da parte dell’occhio umano dell’oggetto in questione:
- Avendo a disposizione, sul bordo della carta, dei riferimenti relativi
alle coordinate geografiche (o ad un qualsiasi sistema di coordinate),
si può sapere immediatamente dove si trova l’oggetto. Se si vuole
conoscere con maggiore precisione la sua posizione, si può invece
prendere una squadra per effettuare delle misurazioni sulla carta.
- Non c’è bisogno di alcuna informazione aggiuntiva esplicita
per capire che i quattro vertici ed i quattro lati del rettangolo formano
un oggetto unico.
- Non c’è bisogno di alcuna informazione aggiuntiva esplicita
nemmeno per capire che, in effetti, si tratta di un rettangolo. La mente
umana sa per esperienza che l’oggetto è un quadrangolo e può
intuire, sempre per esperienza, che i suoi quattro angoli sono degli angoli
retti (se si ha qualche dubbio si può comunque sempre ricorrere
a delle misurazioni).
- Se a lato della carta è riportata una legenda, si può
facilmente creare un’associazione tra gli stili grafici riportati in legenda
e quelli incontrati sulla carta, per cui sarà abbastanza facile
stabilire se il rettangolo in questione rappresenta un edificio, una piscina,
un giardino recintato o altro. Nel caso di una carta tecnica o topografica,
i segni ed i simboli grafici adottati sono spesso talmente intuitivi che
non ci sarebbe nemmeno bisogno di consultare la legenda (della quale in
ogni modo non si deve mai fare a meno!).
Per quanto riguarda, invece, la sua percezione da parte di un
calcolatore, si devono considerare le seguenti questioni:
- Per ogni punto o vertice rappresentato, si devono indicare al calcolatore
le coordinate x, y e, nel caso di disegni tridimensionali,
z. Non è invece necessario definire a priori i valori minimi
e massimi che tali coordinate possono assumere; il calcolatore potrà
facilmente controllare tutti i valori forniti e quindi impostare automaticamente
l’estensione della carta numerica.
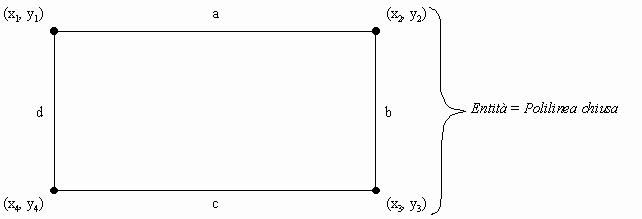
Figura 1: Le informazioni che occorre fornire al calcolatore
per disegnare un rettangolo
- È necessario indicare l’ordine con cui il calcolatore
deve interpretare la serie di coordinate fornite. Nel caso di un triangolo
un qualsiasi ordine produce ovviamente sempre una figura significativa.
Nel caso di quadrangoli, invece, potrebbero verificarsi delle spiacevoli
sorprese che, aumentando ancora il numero di vertici considerati, diventerebbero
del tutto imprevedibili.
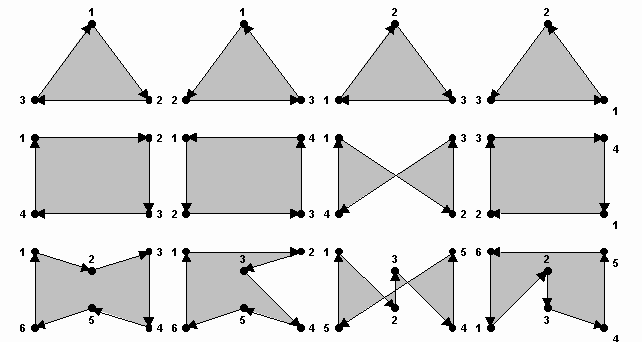
Figura 2: Ordine (sequenza) di interpretazione di una
serie di coordinate
- La terza grandezza indispensabile alla gestione numerica degli oggetti
grafici riguarda il modo di interpretare una serie di coordinate, ossia
la definizione dell’entità grafica trattata. L’elenco
ordinato di una serie di coordinate non definisce in modo univoco quale
tipo di oggetto grafico si intende rappresentare, per cui il calcolatore
deve essere anche informato se si tratta semplicemente di un insieme di
punti nello spazio, di una linea con più segmenti (polilinea),
di un perimetro di una superficie (polilinea chiusa) o, infine,
di una stessa superficie (oggetto bidimensionale).
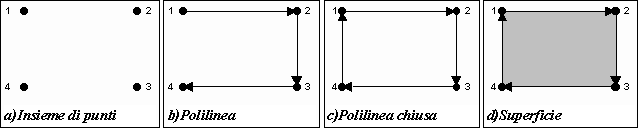
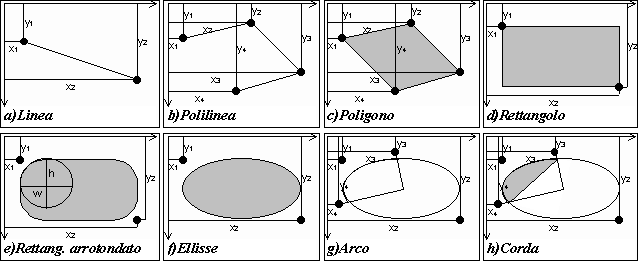
Figura 3: Modi di interpretare un insieme ordinato
di coordinate (concetto di entità)
2.1. Le Entità
Grafiche di Microsoft Windows
La classificazione delle entità riconosciute può tuttavia
variare anche in modo sostanziale da un software all’altro. Così,
per esempio, le librerie grafiche di Microsoft Windows
- utilizzate da moltissimi programmi di grafica per questo sistema operativo
- prevedono le seguenti otto differenti entità.
2.2. Le Entità Grafiche
di AutoCAD
Si può costatare immediatamente come queste categorie non corrispondono
affatto a quelle solitamente utilizzate nella geometria, così come
Windows non distingue tra oggetti mono- e bidimensionali (tra linee perimetrali
e superfici). Per questo, i programmi di disegno professionale fanno pochissimo
uso delle librerie di Windows procedendo invece alla definizione di entità
grafiche proprie. Il software AutoCAD concepisce le seguenti
dieci entità fondamentali.
- Punti (points): una sola coppia (o terna) di coordinate,
ovvero un oggetto adimensionale (senza dimensione) nello spazio bi- o tridimensionale.
- Linee (lines): due coppie (o terne) di coordinate ordinate
unite da un solo segmento di linea (oggetto monodimensionale nello spazio
bi- o tridimensionale).
- Polilinee 2D (2D-polylines): tre o più coppie
di coordinate ordinate (più eventualmente una sola coordinata z
per l’intero oggetto) unite da due o più segmenti di linea (oggetto
monodimensionale nello spazio bidimensionale). La polilinea 2D può
successivamente essere ruotata anche nello spazio tridimensionale mantenendo
tuttavia sempre i vertici posizionati su un piano. Esistono poi cinque
diverse regole per tracciare i segmenti tra due punti di una polilinea:
il congiungimento diretto e quattro funzioni di curva ("normale",
"quadratica", "cubica" e "Bézier").
- Polilinee 2D chiuse (closed 2D-polylines): nelle polilinee
2D chiuse viene tracciato un ulteriore segmento di linea dall’ultimo al
primo vertice. Anche qui possono essere applicate le cinque funzioni di
congiungimento dei vertici.
- Polilinee 3D (3D-polylines): tre o più terne di
coordinate ordinate unite da due o più segmenti di linea (oggetto
monodimensionale nello spazio tridimensionale). A differenza dei vertici
di una polilinea 2D, quelli di una polilinea 3D possono assumere una qualsiasi
dislocazione nelle tre dimensioni.
- Polilinee 3D chiuse (closed 3D-polylines): Anche qui
vengono semplicemente uniti l’ultimo ed il primo vertice con un ulteriore
segmento di linea.
- Archi (arcs): tre coppie di coordinate (più eventualmente
una sola coordinata z per l’intero oggetto) che definiscono in modo
univoco un cerchio, di cui la prima e l’ultima coppia di coordinate segnano
l’inizio e la fine dell’arco di cerchio (oggetto monodimensionale nello
spazio bidimensionale). Come nel caso delle polilinee 2D, l’oggetto deve
sempre rimanere applicato ad un piano.
- Cerchi (circles): una terna di coordinate (centro del
cerchio) più un valore per il raggio (oggetto monodimensionale nello
spazio bidimensionale). Anche il cerchio deve sempre fare riferimento ad
un piano.
- 3D-facce (3D-faces): quattro terne di coordinate ordinate
unite da quattro segmenti di linea a definizione del perimetro di una superficie
piana (oggetto bidimensionale nello spazio tridimensionale). Questa particolare
entità di AutoCAD rappresenta qualche illogicità dal punto
di vista geometrico: concepita come entità planare di base per comporre
approssimazioni di superfici complesse che si sviluppano nello spazio tridimensionale
(come per esempio le superfici curve "a sella di cavallo", ma
anche quelle sferiche), il modo adeguato risultò quello di suddividere
queste superfici complesse in un reticolo a maglie quadrangolari (vedi
sotto). Le unità di base - che dovevano tuttavia rimanere liberamente
manipolabili in x, y e z
- possono così facilmente assumere delle forme geometricamente
impossibili. Basti ricordare che, per definire una superficie planare con
quattro vertici nello spazio tridimensionale, è sufficiente definire
le terne di coordinate di tre vertici e due coordinate (x e y,
x e z oppure y e z) del quarto vertice; la
terza coordinata del quarto vertice è invece in funzione degli altri
undici valori. Essendo invece possibile assegnare alla dodicesima coordinata
un valore qualsiasi, la superficie che unisce il perimetro della figura
deve essere necessariamente una superficie curva di cui però non
si conosce la funzione geometrica.
- Reticoli 3D (3D-meshes): una serie, organizzata come
matrice bidimensionale, di insiemi di quattro terne di coordinate ordinate
unite ciascuno da quattro segmenti di linea (oggetto bidimensionale nello
spazio tridimensionale). Se ad una tale struttura si applica il comando
"esplode" (suddivisione di un "blocco" nei suoi oggetti
di base) si ottengono m·n 3D-facce, dove m
è il numero di righe ed n il numero di colonne della matrice
che struttura il reticolato.
Per quanto riguarda, invece, gli oggetti tridimensionali nello spazio
tridimensionale (i solidi), la cosa si complica ulteriormente.
Poiché però - almeno allo stato
attuale delle cose - la terza dimensione è di relativamente
scarso interesse nei GIS, si può anche fare a meno di approfondire
questo aspetto.
2.3. Le Entità Grafiche
di Arc/Info
Passando infine ai software GIS, si può dire che
le strutture tornano ad essere un po’ più semplici
e - cosa fondamentale - più fedeli ai concetti noti dalla
geometria. Il software Arc/Info
- la cui struttura di dati sarà quella di
riferimento per tutto il corso - utilizza come entità adimensionali
- punti (points) e
- nodi (nodes),
come entità monodimensionali
- archi (arcs),
- percorsi (routes) e
- sezioni (sections)
e come entità bidimensionali
- poligoni (polygons) e
- regioni (regions).
Conviene qui approfondire un po’ di più la questione e non limitarsi
solamente a brevi descrizioni di queste entità.
3.
Quali Sono le Esigenze di Strutturazione dei Dati in un GIS?
Volendo informatizzare, per esempio, una carta catastale (solamente
la suddivisione in lotti), con un programma grafico di Windows o con AutoCAD
si procederebbe probabilmente a definire un poligono per ogni singolo lotto.
Ma il primo problema nascerà appena si procederà ad archiviare
un lotto adiacente ad un altro lotto già memorizzato: l’utente non
avrà altra scelta che archiviare due o più volte quei vertici
che fanno contemporaneamente parte di più di un poligono (lotto).
La soluzione che offre Arc/Info (ma anche altri software GIS) è
quella di organizzare in modo completamente differente i dati: un poligono
non è definito da un insieme ordinato di coppie di coordinate unite
da segmenti, ma - esattamente come lo concepisce
la geometria - da un insieme di entità con una dimensione
in meno. Ovvero:
- un segmento di linea (oggetto monodimensionale) è
delimitato da due punti (oggetti adimensionali),
- una superficie (oggetto bidimensionale) è delimitato
da tre o più segmenti di linea (oggetti monodimensionali), e
- un volume (oggetto tridimensionale) è delimitato
da quattro o più superfici (oggetti bidimensionali).
Questo modo di concepire gli oggetti grafici, la cui presenza indica
solitamente che si tratta di un software GIS e non di una altro tipo di
software grafico, viene chiamato struttura topologica.
3.1 La Topologia nei GIS
La topologia è, prima di tutto, un concetto utilizzato dalla
matematica. Un oggetto grafico può essere descritto sia a mezzo
di informazioni metriche che a mezzo di informazioni non
metriche. Le informazioni non metriche (informazioni topologiche)
forniscono risposte a domande riguardanti le relazioni spaziali tra più
oggetti grafici, come la vicinanza, la contiguità e così
via.
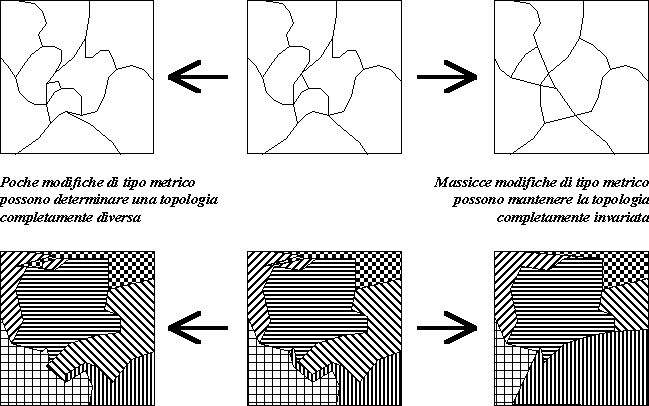
Figura 5: Differenze tra informazioni metriche e topologiche
Se quindi i software GIS utilizzano - come la matematica e, in fondo,
anche l'intuito umano - queste informazioni non metriche per organizzare
i dati grafici, allora nei GIS ci dovrà necessariamente essere un
meccanismo per comunicare al calcolatore che una determinata linea fa parte
di più di un poligono, così come ci dovrà essere un
meccanismo per comunicare che un determinato nodo è il punto iniziale
o finale di più di una linea. A questo proposito vengono predisposte
delle cosiddette tabelle degli attributi per le varie entità
grafica corrispondenti alle dimensioni spaziali utilizzate. Nel software
Arc/Info, che gestisce oggetti grafici fino a due dimensioni (punti, line
e superfici) esistono le seguenti tabelle degli attributi.
- Tabella degli attributi dei nodi (node attribute table, NAT):
è l’elenco completo di tutti i nodi presenti nella carta numerica.
- Tabella degli attributi degli archi (arc attribute table,
AAT): è l’elenco completo di tutte le linee presenti nella carta
numerica. In questa tabella sono presenti alcuni campi, di cui quattro
di particolare interesse:
1. Il campo "FNODE#" (from-node) contiene il numero di
identificazione del nodo in corrispondenza del punto iniziale della linea.
2. Il campo "TNODE#" (to-node) contiene il numero di identificazione
del nodo in corrispondenza del punto finale della linea.
3. Il campo "LPOLY#" (left-polygon) contiene il numero
di identificazione del poligono situato a sinistra della linea.
4. Il campo "RPOLY#" (right-polygon) contiene il numero
di identificazione del poligono situato a destra della linea.
- Tabella degli attributi dei poligoni (polygon attribute table,
PAT): è l’elenco di tutti i poligoni (superfici) presenti nella
carta numerica.
A partire dall’insieme delle linee (dei confini tra poligoni) è
così possibile risalire sia ai nodi che delimitano i singoli archi,
sia ai poligoni che gli archi delimitano a loro volta. Queste relazioni
tra le tabelle delle differenti entità vengono chiamate relazioni
topologiche. Come già accennato prima, le informazioni topologiche,
a differenza delle informazioni metriche, non dicono nulla su quant’è
estesa una superficie, quant’è lungo il suo perimetro, e così
via. Esse descrivono invece come si rapportano spazialmente tra di loro
superfici, linee e punti. Per esempio una rete stradale può essere
modificata metricamente accorciando determinati tratti tortuosi pur lasciando
invariata la sua topologia. La stessa cosa può avvenire per il catasto:
i confini possono essere tracciati in modo diverso, ma le informazioni
topologiche non devono necessariamente per questo subire delle modifiche.
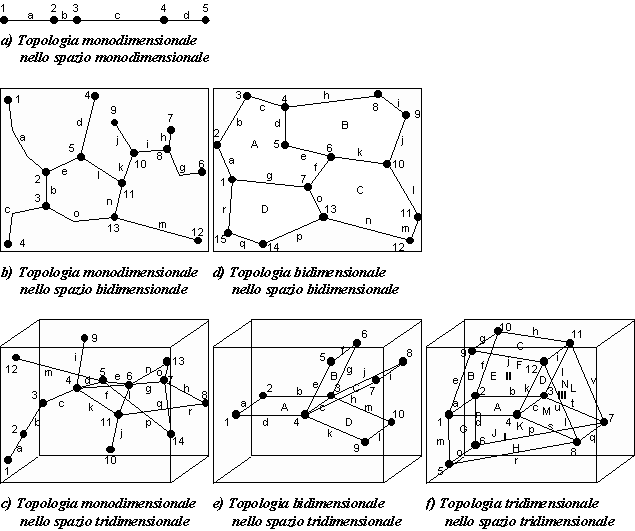
Figura 6: Impianti topologici con una, due e tre dimensioni
Possono quindi esistere più tipi di relazioni topologiche
a seconda del numero di dimensioni presente in un dato insieme di dati
geometrici e a seconda del numero di dimensioni presente negli oggetti
considerati.
- Oggetti monodimensionali nello spazio monodimensionale
(un insieme di segmenti di linea lungo una linea): le relazioni topologiche
stabiliscono quali segmenti si incontrano in quali nodi. Ovviamente ogni
segmento di linea può incontrare al massimo altri due segmenti collocati
ai due punti finali (nodi) del segmento. Benché teoricamente possibile,
un impianto di questo genere non ha chiaramente alcun significato per le
descrizioni di dati geografici.
- Oggetti monodimensionali nello spazio bidimensionale
(un insieme di segmenti di linea collocati su un piano di riferimento):
le relazioni topologiche stabiliscono anche qui quali segmenti si incontrano
in quali nodi. Non esistono limitazioni al numero di segmenti che possono
convergere in un unico nodo, essendo infinite le possibili direzioni di
partenza da un punto nello spazio bidimensionale. Esempi di questi impianti
possono essere reti (come le reti stradali) e grafi
(come le condutture fognarie), ma anche insiemi di confini
che determinano l’articolazione
- Oggetti monodimensionali nello spazio tridimensionale
(un insieme di segmenti di linea collocati all’interno di un volume): le
relazioni topologiche stabiliscono di nuovo quali segmenti si incontrano
in quali nodi. Un impianto logico di questo genere è importante
per gestire, per esempio, le reti stradali con intersezioni a più
livelli (cavalcavia). Poiché però molti software
GIS non gestiscono, come si è già detto, la terza dimensione,
l’utente dovrà costruire un nodo in corrispondenza del cavalcavia
(della sua proiezione sul piano di riferimento) e ‘spiegare’ al calcolatore
che il nodo in questione connette solamente il segmento a con c
ed il segmento b con d, ma non a con b e c
con d. Per facilitare queste operazioni, spesso i software GIS dispongono
di appositi moduli per la gestione delle reti (networks).
- Oggetti bidimensionali nello spazio bidimensionale (un
insieme di superfici collocate su un piano di riferimento): le relazioni
topologiche stabiliscono quali superfici si incontrano in quali segmenti
di confine e, come illustrato al punto 2, quali segmenti di confine si
incontrano in quali nodi (di confine). L’esempio più spesso citato
nella letteratura del settore è quello di una carta dell’uso del
suolo, dove l’intera superficie di riferimento (la carta, l’unità
amministrativa descritta o altro) è coperta da un mosaico continuo
di superfici. Ma anche impianti discontinui, come le carte degli edifici
(delle superfici coperte), ricadono entro questa categoria, sebbene esista
un’ampia regione dello spazio descritto che non è definita esplicitamente
come poligono (questa regione viene spesso chiamata poligono universo).
- Oggetti bidimensionali nello spazio tridimensionale (un
insieme di superfici collocate all’interno di un volume): le relazioni
topologiche stabiliscono anche qui quali superfici si incontrano in quali
segmenti di confine e quali segmenti di confine si incontrano in quali
nodi (di confine). La differenza rispetto al punto precedente è
che in un segmento di confine possono incontrarsi anche più di una
superficie. Topologie di questo genere non vengono, di solito, gestite
dai GIS, anche perché la realtà non offre molte possibilità
di essere descritta in questo modo.
- Oggetti tridimensionali nello spazio tridimensionale
(un insieme di volumi collocati all’interno di un volume): le relazioni
topologiche stabiliscono quali volumi si incontrano in quali superfici
dedotte (superfici di confine), quali superfici dedotte si incontrano in
quali segmenti di linea dedotte (confini, per così dire, di secondo
ordine) e quali segmenti di confine si incontrano in quali nodi (‘confini’
di terzo ordine). È questo sostanzialmente l’impianto topologico
che vige nella realtà materiale che ci circonda. Tuttavia, soltanto
un numero molto ristretto di software GIS gestisce topologie di questo
genere, anche perché la quantità di dati che deve essere
amministrata diventa enorme e le procedure di controllo dell’integrità
delle informazioni topologiche diventano piuttosto complesse e lunghe.
Per descrivere situazioni siffatte (e difficili da proiettare semplicemente
su un piano bidimensionale di riferimento), l’utente dovrà inventarsi
non poche procedure di analisi spaziali, ricorrendo spesso anche alla scrittura
di appositi programmi più o meno grandi.
Oltre a questi sei tipi di impianti topologici, la fantasia (e la matematica)
non pongono alcun limite logico a concepire oggetti e spazi con più
di tre dimensioni. Per esempio il tempo può essere
visto come una quarta dimensione: un solido può cambiare forma nel
tempo e confinare, prima, con un certo numero di altri solidi e, dopo,
con altri solidi ai quali prima non confinava. Oppure: eliminando la terza
dimensione e considerando solamente le prime due più la quarta,
la costruzione di un atlante storico numerico può essere una vera
sfida. L’Italia, per esempio, confinava nel 1914 alla Francia, alla Svizzera,
alla Repubblica di San Marino, all’Austria-Ungheria e al mare; nel 1939,
al posto dell’Austria-Ungheria, c’erano Austria e Jugoslavia; oggi, al
posto della Jugoslavia, c’è la Slovenia. Alcune zone, che nel 1914
facevano parte del poligono "Austria-Ungheria", nel 1939 facevano
parte del poligono "Jugoslavia", altre del poligono "Italia",
altre ancora di altri poligoni. Alcune zone, che nel 1939 facevano parte
del poligono "Italia", oggi fanno parte del poligono "Francia",
altre del poligono "Slovenia" e altre ancora del poligono "Croazia".
Il 7 giugno 1929, poi, venne costruito un nuovo (piccolo) poligono ‘tagliando’
un pezzo dall’Italia e dandogli il nome "Stato della Città
del Vaticano". È facile immaginarsi quanto complicate dovrebbero
essere queste relazioni topologiche spazio-temporali.
Sono possibili però anche impianti topologici a n
dimensioni. Se, nell’atlante storico numerico, si volessero includere
anche informazioni che rispondono a domande come "Che cosa sarebbe
accaduto se tra il 1991 e il 1993 non si fosse smembrata la Jugoslavia?"
allora si dovrebbero disegnare almeno due carte politiche per la situazione
odierna: una che riporta la situazione odierna così com’è
effettivamente oggi e una che riporta la situazione odierna se non fosse
cambiato nulla; ma affermare che "la Jugoslavia non si è smembrata"
non significa affermare "la Jugoslavia non è cambiata",
per cui le possibili situazioni odierne sono infinite. E ciò equivale
a dire che il nostro atlante dovrà avere un impianto topologico
a cinque dimensioni. Poiché però le situazioni nodali (i
momenti in cui la nostra fanta-storia si suddivide in due ‘correnti temporali’)
possono a loro volta essere infinite, l’impianto topologico dell’atlante
storico/fanta-storico dovrà addirittura essere necessariamente ad
infinite dimensioni!
Che queste dissertazioni non sono semplicemente degli esercizi di logica
fine a sé stessi, può facilmente essere sperimentato quando
un progettista di GIS dovrà affrontare la questione dell’elaborazione
di scenari futuri dello sviluppo di un determinato territorio.
L’argomento, però, non può essere trattato in modo soddisfacente
in questa sede.
3.2. La Struttura
Topologica dei Dati in Arc/Info
Partendo dagli oggetti grafici senza dimensione spaziale (oggetti a
zero dimensioni), Arc/Info concepisce due entità adimensionali
(puntuali) distinte: i punti e i nodi. Un "punto" è semplicemente
una coppia di coordinate che può essere utilizzata per simboleggiare
un oggetto troppo piccolo per essere rappresentato alla scala di visualizzazione,
mentre un "nodo" è invece un punto definito come limite
di un segmento di linea. In altre parole
- un "punto" è un elemento puntuale per
convenzione (nella realtà bidimensionale della carta dovrebbe
in teoria essere una superficie, ma si conviene a rappresentarlo
come punto), e
- un "nodo" è un elemento puntuale per
deduzione (poiché si tratta dell’inizio o della fine di
una linea, si deduce che in quel determinato luogo si trova il primo
o l’ultimo degli infiniti punti che formano la linea).
Per le entità monodimensionali (lineari), invece,
la distinzione in elementi per convenzione ed elementi per deduzione purtroppo
non si riflette più così direttamente nella struttura di
dati. È tuttavia anche qui essenziale tenere presente che una linea
("arco") può essere definita sia come segno convenzionale
di un oggetto realmente esistente, sia come confine tra due
aree che ovviamente non ha alcuna corrispondenza nella realtà, se
non quella di indicare l’insieme di punti che appartengono contemporaneamente
a due superfici. Ciononostante, Arc/Info non si limita ad una sola entità
monodimensionale, ma ne distingue ben tre ("archi", "sezioni"
e "percorsi") per venire incontro ad esigenze di strutturazione
degli elementi lineari di cui si parlerà tra breve.
Per le entità bidimensionali (zonali), infine,
non vi è alcuna necessità di distinguere tra oggetti per
convenzione e oggetti per deduzione. La presenza di superfici per deduzione
significherebbe, infatti, che il modello di dati gestisce anche oggetti
tridimensionali (un confine tra due volumi è una superficie), cosa
che per i dati vettoriali di Arc/Info non è il caso. Anche qui però,
i programmatori di Arc/Info sono venuti incontro a particolari esigenze
di organizzare gli elementi zonali (poligonali).
Riepilogando, le "coperture" (disegni vettoriali
con impianto topologico) di Arc/Info prevedono la presenza delle seguenti
entità grafiche.
- Punti (points): sono semplicemente delle coppie di coordinate
(Arc/Info lavora solo in due dimensioni, almeno per quanto riguarda la
struttura dei dati). La tabella degli attributi che viene associata si
chiama PAT (Point Attribute Table) che funge anche da tabella
degli attributi poligonali come si vedrà tra poco. Attraverso un
campo identificatore si possono creare relazioni con altre tabelle costruite
dall’utente. Sulla tecnica del relazionamento che definisce un utente (che
è diversa da quella che instaura le relazioni topologiche), si dirà
qualcosa più avanti.
- Nodi (nodes): anche i nodi sono coppie di coordinate.
L’utente non può però definire liberamente un nodo, in quanto
un nodo viene creato automaticamente quando l’utente inizia e finisce col
disegnare una linea o quando dà il comando di creare un’intersezione
tra due linee. La loro tabella degli attributi si chiama NAT
(Node Attribute Table).
- Archi (arcs): sono degli insiemi di segmenti di linea.
Un segmento di linea è costituito da due coppie di coordinate unite
tra di loro. Due segmenti di linea si incontrano in un terzo tipo di punto,
chiamato vertice (vertex), la cui struttura rimane però quasi completamente
nascosta all’utente che vi può accedere solamente attraverso pesanti
operazioni di programmazione. L’unità logica è quindi l’arco,
la cui tabella degli attributi si chiama AAT (Arc Attribute Table)
e che riporta gli identificatori nella NAT del nodo di partenza (from-node,
campo FNODE#) e di quello di arrivo (to-node,
campo TNODE#), gli identificatori nella
PAT poligonale (vedi punto 6) del poligono di sinistra (campo LPOLY#)
e di quello di destra (campo RPOLY#), e
la lunghezza dell’arco (campo LENGTH).
- Sezioni (sections): sono parti di archi. Una sezione
comincia ad una determinata distanza (che può essere anche zero)
dal nodo di partenza dell’arco al quale appartiene, e finisce al nodo finale
o prima del nodo finale. La tabella associata di chiama SEC (Section
Table) e contiene l’identificatore nella RAT (vedi sotto) del percorso
al quale appartiene (campo ROUTELINK#),
l’identificatore nella AAT dell’arco al quale appartiene (campo ARCLINK#),
le posizioni iniziale (campo F-POS) e finale
(campo T-POS) relative all’arco espresse
in percentuale di lunghezza dell’arco, e le posizioni iniziale (campo F-MEAS)
e finale (campo T-MEAS) relative al percorso.
Poiché un insieme di archi può dare luogo a diversi sistemi
di percorsi e sezioni, ogni SEC è in realtà una collezione
di tabelle più che una tabella unica. Un singolo sistema di sezioni
si chiama sottoclasse (subclass) e la tabella specifica si
chiama SEC<subclass>, dove al posto di <subclass> va inserito
il nome che l’utente attribuisce alla sottoclasse in questione.
- Percorsi (routes): sono collezioni di sezioni, dove le
sezioni di un singolo percorso devono formare un oggetto lineare ininterrotto
(pensando, per esempio, al percorso che compie un autobus di linea). La
tabella degli attributi associata si chiama qui RAT (Route Attribute
Table) che è organizzata per sottoclassi in corrispondenza di
singoli sistemi di percorso (route systems).
- Poligoni (polygons): a differenza dei software grafici
di Windows e dei programmi per il CAD, i software GIS che gestiscono impianti
topologici bidimensionali non necessitano di strutture complesse di vertici
e segmenti di linea per definire un poligono, ma semplicemente di un punto
(una coppia di coordinate) chiamato centroide (centroid)
o etichetta (label o label point). Nelle procedure
di ricostruzione dell’impianto topologico, il software effettua una ricerca
attraverso l’intero database geografico per assegnare ai campi LPOLY#
e RPOLY# della AAT gli identificatori giusti
dei singoli centroidi. Per questo motivo, punti e poligoni (o meglio punti
e centroidi) condividono una stessa tabella degli attributi, la PAT,
che, nel caso si tratti di punti per convenzione, viene chiamata Tabella
degli Attributi Puntuali (Point Attribute Table) e, nel caso si tratti
di punti astratti quali i centroidi dei poligoni, Tabella degli Attributi
Poligonali (Polygon Attribute Table). La PAT contiene in ogni caso
un campo AREA (superficie del poligono)
e PERIMETER (lunghezza del perimetro =
somma delle lunghezze degli archi che compongono il perimetro). Nelle PAT
puntuali, questi due campi sono ovviamente per tutti i record uguali a
zero.
- Regioni (regions): sono collezioni di poligoni. Ogni
regione può essere costituita da uno o più poligoni che non
necessariamente devono essere contigue tra di loro. L’utilità di
questa entità si comprende facilmente se si tenta di costruire una
carta politica numerica dell’Italia. Ogni singolo Comune può essere
rappresentato come poligono. Dopodiché, questi poligoni possono
essere aggregati per formare le Province: ogni Provincia sarà una
regione, e l’insieme delle Province formerà la sottoclasse "Province"
di questa struttura di dati. La tabella degli attributi delle regioni è
semplicemente un’estensione della PAT poligonale, in modo analogo a quella
delle sezioni. Nel caso della sottoclasse "Province" la tabella
in questione si chiamerà "PATProvince" e riporterà
gli stessi campi della PAT. Poi si possono ovviamente definire anche altre
sottoclassi, sia in base ai poligoni che in base ad una sottoclasse di
regioni già definita. Nell’esempio della carta politica dell’Italia,
un’altra sottoclasse di regioni potrebbe essere formata dall’aggregazione
di singole Province per dare luogo alle venti Regioni d’Italia: la tabella
degli attributi in questione potrebbe quindi chiamarsi "PATRegioni".
Non ci sono limiti a definire un numero qualsiasi di sottoclassi in corrispondenza
di aggregazioni di poligoni e regioni. L’entità delle regioni facilita
inoltre anche la gestione di enclaves ed esclaves:
in Italia esiste anche un elevato numero di Comuni il cui territorio non
è sempre contiguo, sia per la presenza delle isole fisiche sia di
quelle amministrative. Definendo fin dall’inizio come regioni anche i Comuni
(con una "PATComuni"), sarà possibile gestire come unità
indistinte anche i Comuni composti da più pezzi staccati tra loro.
Pagina creata il 19 marzo 1997 e modificata il 21 aprile 1997
Per informazioni potete contattarmi all'indirizzo hedorfer@cidoc.iuav.unive.it